
TUT Game Lab
Tampere University of Technology, Pori department
Email: antero.lindstedt@tut.fi
TUT Game Lab
Tampere University of Technology, Pori department
Email: kristian.kiili@tut.fi
TUT Game Lab
Tampere University of Technology, Pori department
Email: pauliina.tuomi@tut.fi
TUT Game Lab
Tampere University of Technology, Pori department
Email: arttu.perttula@tut.fi
Game-based learning solutions provide possibilities to teach conceptual number knowledge in engaging ways. The evaluation of user experience and error-proneness of the user interface are crucial in the educational game development process and game-based assessment. In the present study, we investigated how two different user interfaces of the rational number game, Semideus, influenced the game character controlling accuracy and user experience. Two user interfaces varying in the intensity of physical activities needed for controlling the game character were compared. Thirty-six university students played both Semideus game versions for 20 minutes in randomized order. In order to compare the tilting (low physical intensity) and walking (high physical intensity) user interfaces we used stealth assessment as an objective measure of controlling accuracy as well as flow experience and playability questionnaires as subjective measures of user experience. The results revealed that there was no significant difference in game controlling accuracy between the user interface solutions, suggesting that the intensity of the physical activities did not influence the error-proneness. However, the subjective measures indicated that students appreciated the tilting user interface significantly more than the walking user interface. Implications of the findings for future research and further development of the Semideus game are discussed.
Keywords: user experience, user interface, embodied cognition, math, fractions, game, learning, education
A good sense of rational numbers creates the foundations for advanced mathematics. However, research in cognitive psychology and mathematics education has revealed that children and even educated adults struggle with understanding of rational numbers (Van Dooren, Lehtinen, & Verschaffel, 2015). There is a great deal of evidence that even after considerable mathematics instruction many learners fail to perform adequately even in simple fraction tasks (Siegler et al., 2013; Siegler et al., 2011; Stafylidou & Vosniadou, 2004). Mathematics education researchers have admitted that most of the students’ difficulties with rational numbers can be attributed to inadequate instruction (Vamvakoussi & Vosniadou, 2010). The problem is that the recent advances in modelling numerical development have not been exploited to practices of teachers and the instruction tends to emphasize procedural instead of conceptual knowledge (Bailey, Siegler & Geary, 2014). Given the widespread difficulties that people face with fractions, traditional instructional methods should be reconsidered and complemented by new tools for fostering fraction knowledge.
Game-based learning solutions may provide possibilities to teach conceptual number knowledge in engaging way. In this article we consider the design of a Semideus rational number game that is founded on recent advances in numerical development research (McMullen et al., 2014; Torbeyns et al., 2014; Siegler et al., 2011; Ni & Zhou, 2005) and theories that provide an account for the use of manipulatives in digital learning materials (Pouw, Van Gog & Paas, 2014). The main aim of this article is to study the user experience of two different user interfaces of Semideus game. Both user interfaces are based on embedded embodied cognition, but the intensity of physical activities needed for controlling the game varies. The optimization of user experience is important because the previous research have shown that subjective playing experience is positively connected with playing performance and learning outcomes (Kiili, Perttula & Arnab, 2014). We selected flow theory as a game quality measure because flow seems to have a positive influence on performance enhancement, learning, and engagement (e.g. Csikszentmihalyi et al., 2005; Engeser & Rheinberg, 2008) and for example Kiili et al. (2014) have successfully used flow for analyzing the quality of serious games.
Flow describes a state of complete absorption or engagement in a specific activity in which a person excludes all irrelevant emotions and thoughts (Csikszentmihalyi, 1990; Csikszentmihalyi, 2002). During the optimal experience, a person is in a positive psychological state where he or she is so involved with the goal-driven activity that nothing else seems to matter. An activity that produces such experiences is so pleasant that the person may be willing to do something for its own sake, without being concerned with what he will get out of his action. This kind of intrinsic motivation is very important especially in serious games that usually require different cognitive or physical investments compared to entertainment games.
In this article we will first shortly present the theoretical background of the Semideus game following with a description of the game. Second, we will report the results of a study in which the two different user interfaces of the Semideus game were compared in terms of game character controlling accuracy and playing experience. Third, we will consider the further development of the Semideus game user interface according to the results of this comparison study.
2.1 Development of rational number knowledge
One approach used to explain children's difficulties in learning rational numbers is the whole number bias Ni & Zhou, 2005). Whole number bias suggests that common misconceptions about rational numbers originate from the false belief that all properties of whole numbers can be applied to rational numbers. For example, when comparing fraction magnitudes, people sometimes think that the fraction that has larger whole numbers as parts is larger (e.g. one may think that 1/5 is larger than 1/3, because 5 is larger than 3. According to Alibaliv and Sidney (2015) the whole number bias has been observed in elementary school students, in high school students, in adults, and even in expert mathematicians. Thus, the bias is evident also in people who are extensively familiar with rational numbers and everybody can benefit from numerical trainings.
Siegler et al. (2011) have argued that theories of numerical development have emphasized too much the whole number bias and how it interferes with fraction learning. To support this argument Siegler et al. (2011) proposed an integrated theory of numerical development that emphasizes continuity between acquisition of understanding whole numbers and fractions. According to their theory significant conceptual change is required to understand that fractions, like whole numbers, represent magnitudes that can be located on number lines (Siegler et al., 2011). In line with integrated theory of numerical development McMullen et al., 2014) have shown that successful conceptual change with rational numbers is rare and hard to come by. In fact, the recent findings have suggested that instructional interventions that aim to support conceptual change should target learners’ interpretation of rational numbers as magnitudes by practicing them on number lines (Torbeyns et al., 2014; Bailey, Siegler & Geary, 2014; Fuchs et al., 2013). These findings are in line with an integrated theory of numerical development and thus we have used the theory as a starting point to design our Semideus game.
2.2 Embedded embodied cognition and learning manipulatives
Games provide an appropriate environment for implementing features of virtual manipulatives that rely on embedded embodied cognition approach proposed by Pouw, Van Gog & Paas (2014). According to Moyer et al. (2002) virtual manipulatives are interactive Web-based visual representations of dynamic objects that present opportunities for constructing mathematical knowledge. Virtual manipulatives are argued to be effective in mathematics instruction because they can connect dynamic visual images with abstract symbols (Reimer & Moyer, 2005). For example, the results of (Reimer & Moyer, 2005) have indicated that the virtual fraction manipulatives can enhance students’ conceptual understanding of fractions and enjoyment in learning mathematics.
The embedded embodied cognition draws together the research on embedded cognition (e.g. Clark, 2008) and embodied cognition (e.g. Barsalou, 2008) in order to guide the design of learning manipulatives. The embedded embodied cognition states that perceptual and interactive richness may provide opportunities for alleviating cognitive load and transfer of learning is not reliant on decontextualized knowledge but may draw on previous sensorimotor experiences stimulated by manipulatives. Moeller et al. (2012) have argued that embodied representations of number (magnitude) exist, are not limited to finger-based representations, and influence on number processing in such a systematic and functional way that it can be used to foster the efficiency of numerical trainings. For example, Cook et al. (2008) found that children who were encouraged to make gestures while learning a new arithmetic strategy benefited from gesturing with respect to retention of knowledge. In line with this, Link et al. (2013) showed that embodied number line training with whole-body movements (Kinect based UI) resulted in better learning outcomes than control training (mouse based UI). The results revealed that embodied training seems to be beneficial in particular for children with lower general cognitive ability and lower working memory capacity. In general, these findings are in line with evidence indicating that the processing of numbers and space are related (Wood & Fischer, 2008).
The mental number line is assumed to be spatially oriented from left-to-right, which might account for the findings about a relationship between numbers and spatial information (Link et al., 2013). For example, in Motion Math game the idea of spatially oriented mental number line is successfully applied by implementing tilting based controls to manipulate fraction magnitudes (Riconscente, 2013). To conclude embedded embodied cognition approach assumes that seemingly abstract representations may be based on bodily experiences and movement may help children to understand abstract concepts better and the perceptual and interactive richness provides opportunities for alleviating cognitive load.
The Semideus game is based on a Semideus research engine. While the base game is always the same, the engine offers numerous options to tweak the game to fit into the current research topic. Most of the adjustments are related to the level design (like types of tasks, number of enemies, and available hints) but some are changes to the game mechanics such as the difference in the controlling methods used in this study.
The Semideus game is designed to support the development of rational number conceptual knowledge. In particular, Semideus addresses the development of two sub-concepts necessary for a complete mathematical understanding of rational numbers, 1) representations of the magnitudes of rational numbers and 2) the density of rational numbers. The idea of the game is grounded on integrated theory of numerical development (Siegler et al., 2011) while it steadily expands understanding of the connection between different number representations and their magnitudes. The understanding is gradually expanded from whole number magnitudes to magnitudes of fraction, decimal and percent numbers.
In this article we focus on two main task types of the game: estimation and ordering tasks. We start with presenting the background story of the game following a description how rational numbers are mapped to the game mechanics and how the user interface is designed to support understanding of rational numbers.
3.1 The story of the game
The thematic setting and graphical outlook relate to the mythology of ancient Greece. In the story Semideus, a son of Zeus, is tasked to seek golden coins Kobalos the goblin has stolen. Kobalos has hidden the coins, as well as traps, to the trails of mount Olympos. Semideus however has found goblin’s notebook, which shows the locations of the coins and traps, encrypted in mathematical symbols, and must race the goblin to retrieve the coins. While collecting the coins, Semideus climbs up the mountain platforms to reach the top where Zeus is eagerly awaiting for his coins.
3.2 From whole number bias to game mechanics
The recent research has suggested that instructional interventions should target learners’ interpretation of rational numbers as magnitudes by practicing them on number lines (Torbeyns et al., 2014). Thus, the gameplay of the Semideus game is founded on tasks that require working with number lines implemented as walkable platforms of the mountain. In the basic version the player can face five different kinds of tasks: magnitude estimation, magnitude comparison, magnitude ordering, and density awareness. Similar tasks are commonly used in rational number studies (Siegler et al., 2011; McMullen et al., 2014), but in Semideus these tasks are embedded into the game mechanics.
In magnitude estimation task Semideus tries to locate a hidden chest on each platform. The values to estimate are shown as mathematical symbols (Figure 1). Semideus finds some coins if he estimates the location accurate enough – if not he loses energy. The estimation accuracy percent determines the amount of coins that Semideus finds from the chest. If Semideus does not manage to locate the correct spot (too low accuracy) he has to try again.

Figure 1. Example of magnitude estimation task. The player has to find the value displayed in the left corner and avoid the value in the right corner
In magnitude comparison task Semideus faces two stone tablets on the platform accompanied with rational number symbols. The task of the player is to organize the tablets on the number line according to their magnitudes before the goblin steals all gold coins from upper platform. In the example (figure 2) the player has to decide whether value 3/5 is larger than value 5/9 and place the tablets to ascending order on the number line. The player can carry the tablets on the platform in order to perform the comparison. The exact places of the tablets on a number line are not relevant, only the order. If the magnitudes of the tablets are the same the player should pile up the tablets. This way the magnitude comparison task can address also the equivalency of rational numbers.
Basically the ordering task is the same task than comparison task, but there are more stone tablets involved (3-5). This task can be designed to support also understanding of density if magnitudes are selected accordingly (e.g. 1/4, 0.3, 1/2, 3/4). In both comparison and ordering tasks, with a correct answer, the player gains all the coins not yet stolen by the goblin. A wrong answer means the player loses some energy and has to try again.

Figure 2. Comparison task
3.3 User interface solutions
Two different user interface solutions were developed for this study. Both versions required some physical activity from the player. The first user interface solution (Tilting UI) required only light gestures. The game character changed his facing direction when the tablet was tilted slightly to either left or right. Further tilting caused the character to walk to the tilted direction. The movement speed was defined by the tilting angle. In the second user interface solution (Walking UI) the facing of the character was controlled in the same way as in the first version. However, the movement of the character required the player to walk in place while holding the tablet in his or her hands. The character’s movement speed increased as the physical movement intensified. In terms of Pouw, Van Gog & Paas (2014), both user interface solutions utilize embedded embodied interactions and thus the solutions can alleviate cognitive load. In general, the character can be considered as a visual manipulative and the tilting gestures and walking on the number line goes beyond mental number line. The increased physical activity has the potential to be beneficial beyond the embedded embodied cognition. Emerging research has shown that exergame interventions in schools can improve academic performance, reduce classroom absenteeism, tardiness, and negative classroom behaviors (Lieberman, et al 2011).
In this study a within-subjects design was used. Each participant played both versions of the game: tilting user interface and walking user interface. The playing order was randomized. The tasks in the game were exactly the same in both versions.
4.1 Participants
This study was executed as part of the Tampere University of Technology’s User-centered design course in the beginning of 2015. The course is a part of the Master’s Degree Programme in information technology.
Overall 45 students participated in the user experience study in which the two user interface solutions were compared. From these 45 students 9 were left out as they did not play both games or filled in the user experience questionnaires inadequately. Of the remaining 36 participants 12 were females and 24 males while the average age was 38.5 years. Even though primary end users of the game are school children of age 11-14, this study was conducted with university students. This was intentional as they should master the mathematical content of the game and thus be able to focus on controlling the game character as accurately as possible and that way this study provides information about the quality of the user interface solutions emphasizing the accuracy of controlling the game character. Moreover, the secondary end users are adults, teacher students and teachers in particular.
4.2 Math items and measures
There were three levels in the Semideus game prototype that was used in this study. The first level included ten whole number estimation items (tasks) on the number line ranging from -50 to 50. The second level included 11 fraction estimation items on the number line ranging from 0 to 5. The third level included nine comparison and ordering items. The whole number tasks could be considered easy for university students and the answers should be pretty accurate. These were the primary tasks for studying the user interface differences as the participants’ mathematical skills should not be a decisive factor. The rational number tasks should provide a little more difficulty even for adults. This way the participants might get some more enjoyment out of the game as there is some challenge in it. The comparison and ordering tasks offered some variation to the game and were somewhere in the middle in terms of the difficulty.
User experience was measured in terms of flow experience (Csikszentmihalyi, 1990; Engeser, 2012) and playability. Flow experience was measured with a 9-item questionnaire, developed by the authors. The items included were derived from flow scale used in Kiili et al. (2014) study. The dimensions included were challenge-skill balance, clear goals, concentration, autotelic experience, loss of self-consciousness, sense of control, and action awareness merging. Playability was measured with a 3-item questionnaire developed by the authors. The dimensions included were ease of use, intuitiveness of the user interface, and controlling accuracy of the user interface. With each dimension a 6-point Likert-type response format was used. Stealth assessment approach was utilized in collecting game performance data. Stealth assessment is an evidence-based approach where assessment is well integrated to the gameplay and the assessment is carried out non-invasively (Shute & Kim, 2014; Shute, 2011). In practice, the game continuously logged playing behavior in a secured server according to defined rational number competence model and from these log files estimation accuracy (error) and comparison performance (correctness) was retrieved. Moreover, the appreciation of the both user interface solutions was studied with 6-point Likert-scale statements (I liked the tilting user interface a lot / I liked the walking user interface a lot.)
4.3 Procedure
The class started with a brief introduction and description of the Semideus game. After that the students were divided into two groups; one group that controlled Semideus by tilting the tablet and one group that controlled the game by walking in place. The game was played in groups of five students. In the beginning of each playing session brief instructions were given and after that the game was played. After each session, in both groups, the participants were asked to fill in a paper based user experience questionnaire (flow and playability items). When the students had played through both game versions they were instructed to evaluate the user interface solutions (appreciation of the user interfaces).
4.4 Data analyses
After the playing sessions, data collected with questionnaires and log files were shifted to SPSS and analyzed. Flow construct (the mean of flow dimensions) and playability construct (the mean of playability dimensions) were computed. Accuracy of number line estimation tasks was analysed according to Percentage Absolute Error (PAE) computed as 100 * abs(estimated value – correct value) / numerical range of the number line. PAE gives values between 0-100% (0% refers to perfect accuracy - in other words estimation error is zero). PAE was computed for both tilting and walking user interface solutions.
5.1 Playing performance
The magnitude estimation tasks were based on two different number lines. A number line ranging from -50 to 50 contained whole number tasks while a number line from 0 to 5 contained fraction tasks. As shown in Table 1, students’ estimates were more accurate on whole number tasks (Tilting UI M = 3.54%, SD = 3.79%; Walking UI M = 5.87%, SD = 8.87%) than on fraction tasks. A paired-samples t-test indicated that there was not a significant difference in the whole number estimation accuracy in tilting UI (M = 3.54%, SD = 3.79%) and in walking UI (M = 5.87%, SD = 8.87%) conditions, t(35)=-1.624, p = .113. Similarly, such a difference was not found either in the fraction estimation accuracy in tilting UI (M = 9.01%, SD = 6.53%) and in walking UI (M = 9.06%, SD = 6.05%) conditions, t(35)= -.265, p = 793.
Table 1. Magnitude estimation accuracy (PAE: Percentage Absolute Error) in different UI versions and task types (N = 36)
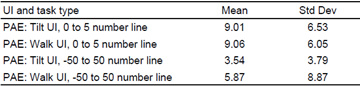
A paired-samples t-test was conducted to compare the comparison performance in tilting and in walking UI conditions. There was not a significant difference in the comparison performance in tilting UI (M = 75.59%, SD = 16.91%) and in walking UI (M = 74.38%, SD= 21.13%) conditions, t(35)=.347, p = .731.
5.2 User experience
The evaluation of user experience is a crucial part of a game development process. The enjoyment level that an educational game offers is a key factor in determining whether a player will be engaged in the gameplay and achieves the desired objectives of the game. Furthermore, controlling the game has to be accurate, so that the controlling of the game does not negatively influence on learning performance. In this study we measured user experience in terms of flow experience and playability (user interface satisfaction). The reliability analysis of the used flow questionnaire (N = 36) indicated that the flow construct was internally consistent (Tilting UI: α = 0.82; Walking UI: α = 0.83), which means that all nine dimensions measured the same phenomenon, flow construct. The internal consistency of playability construct (N = 36) was weaker (Tilting UI: α = 0.62; Walking UI: α = 0.77).
The table 2 shows that players experienced significantly higher flow with tilting user interface (M = 4.30, SD = 0.76) than with walking user interface (M = 3.88, SD = 0.83), t(35) = 3.08, p = .004. The biggest differences were in sense of control t(35) = 2.89, p = .007, action awareness merging t(35) = 2.22, p = .033, and autotelic flow dimensions t(35) = 2.80, p = .008. Table 2 also shows that the playability of tilting version was more appreciated (M = 4.23, SD = 0.81) than playability of walking version (M = 3.36, SD = 1.16), t(35) = 4.45 , p < .001. The biggest difference was in accuracy of game controls dimension. The correlation analysis indicated that there were statistically significant relationships between playability and experienced flow level with both user interfaces (Tilting UI; r = 0.49, p = .002; Walking UI: r = 0.54, p = .001). This means that the playability of the game influence remarkably on overall user experience and the game controls have to be optimized. When participants were asked to evaluate both user interfaces after the playing sessions they appreciated the tilting UI remarkably more (M = 4.47, SD = .76) than walking UI (M = 2.44, SD = 1.24), t(35) = 7.94, p = .000. The large standard deviation of walking UI shows how physically activating controlling mechanism is divisive. Although the difference between user interfaces is large with this measure the result is in line with flow experience and playability findings.
Table 2. Means and standard deviations of the user experience measures in tilting and walking user interfaces (N = 36)
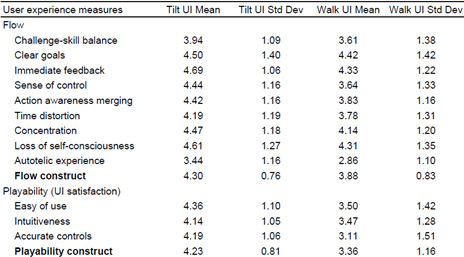
Furthermore, the correlation analysis also indicated that magnitude estimation accuracy (PAE) in walking condition correlated significantly with flow experience, r = -.37, p = .026. However, in tilting condition the correlation was not statistically significant, r = -.31, p = .068.
In general, the results clearly show that the tilting user interface was better with all used measures. Although, the difference in controlling accuracy (PAE) was not large between the tested user interfaces, players experienced the walking user interface more inaccurate than it actually was. If we could facilitate the sense of control and action awareness merging in walking user interface, it could improve the overall user experience significantly.
5.3 Observation notes of playing behavior
The playing behavior was observed during the game playing session. Overall appreciation of Semideus game was positive and participants were eager to play the game. The adaptation of the idea of Semideus was smooth and the playing continued seamlessly. Especially, when playing the game with tilting controls participants got immersed and the controlling gestures did not interfere the overall playing experience. On the contrary, the walking user interface seemed to distract the players a bit mainly in the beginning when the participants were still learning how sensitive and precise the controlling by walking actually was. Walking controls required more concentration from the participants and it influenced negatively on the playing experience from time to time. Based on the question concerning which controlling mode the participants preferred, it can also be seen that the tilting mode was preferred more than the walking mode. It is also worth noting that, after playing the game for a while, most of the players of the walking version reverted to just shaking the device instead of walking in place.
The results revealed that there was not significant difference in game controlling accuracy between the tilting and walking user interfaces, suggesting that the intensity of the physical activities did not influence the error-proneness of the user interface. Despite of that the level of experienced flow and appreciation of the playability of the tilting user interface indicated that students appreciated the tilting user interface significantly more than the walking user interface.
The study showed that walking in place as a controlling method for Semideus game is problematic. It distracted players and caused them to feel less immersed in the game. At the same time however, the use of walking UI did not result in significantly worse answer accuracies. The tilting UI worked much better and the physical activity required to control the character felt natural. This would indicate that the physical controlling itself is not an issue if implemented properly.
The development of Semideus continues by adding more features to the game and by modifying existing features based on the findings from this study. The walking based UI has already been slightly redesigned based on the results of this study. The walking speed of the character was adjusted to be more consistent. Originally the character would stop moving instantly when the player stops walking in place. Now the character continues to move for a short moment with decaying speed even if the player is no longer walking. Now the character moves smoothly also in cases when player’s walking is too subtle (i.e. device’s accelerometer misses some of the input). The downside to this change is that it is harder to stop at the exact point on the number line. To compensate this, the tilting of the device now moves the character similarly to the tilting based UI but it does that only at a snail’s pace. Further speed is gained by walking in place. This makes it easier to fine tune the answer and in terms of flow experience it should facilitate the sense of control and action awareness merging. We are currently running a study with sixth graders in which this new walking user interface is tested.
The fact that most of the players of the walking version of the game started to control the game by shaking the device instead of walking in place is an issue. It is difficult to prevent this technically as the movement is detected using the device’s accelerometers, which does not separate how the motion is generated. On the other hand, since the game contains onscreen buttons, the device must be held on hands. One possible way to prevent this conduction could be to add competitiveness between players by making a multiplayer version of the game. This might add some peer pressure to do things the correct way.
During the testing it was observed that some of the users first tried to tilt the device in a different way than what was expected. They rotated the device similarly to car’s steering wheel. This could be an optional controlling method to add to the game, as it seemed logical to some.
There are several limitations in this study. The sample size (36) was rather small and thus the results cannot be generalized. Furthermore, the participants were not the primary end users and the results might not be fully alike with middle school aged children. Adults may feel differently about physically moving during the game than children do and thus more research with primary end users are needed. The participants played each version of the game for about 20 minutes. This was probably enough to form an opinion about the controlling methods, but still, longer sessions might reveal for example better familiarization or increased exhaustion that might affect the playing experience.
The participants played the game only for a short time on a single session so the effects of different intensity physical activities to learning outcomes or player’s fitness level could not be studied. Despite the negative opinions about the walking user interface there could still be potential in the more physical approach. If the revised version of the walking UI could bring the playability level closer to the tilting UI’s playability, there could be a case for further studies with the Semideus game.
Alibali, M. W., & Sidney, P. G. (2015). Variability in the natural number bias: Who, when, how, and why. Learning and Instruction, 37, 56-61.
Bailey, D. H., Siegler, R. S., & Geary, D. C. (2014). Early predictors of middle school fraction knowledge. Developmental science, 17(5), 775-785.
Barsalou, L.W. (2008). Grounded cognition. Annual Review of Psychology, 59, 617–645.
Clark, A. (2008). Supersizing the Mind: Embodiment, Action, and Cognitive Extension: Embodiment, Action, and Cognitive Extension. New York: Oxford University Press.
Cook, S.W., Mitchell, Z. & Goldin-Meadow, S. (2008). Gesturing makes learning last. Cognition, 106 (2), 1047–1058.
Csikszentmihalyi, M. (1990). Flow: The Psychology of Optimal Experience. New York: Harper Perennial.
Csikszentmihalyi, M. (2002). Flow: The psychology of optimal experience (2nd edition). New York: Harper & Row.
Csikszentmihalyi, M., Abuhamdeh, S., & Nakamura, J. (2005). Flow. In A. Elliot, & C.S. Dweck (Eds.) Handbook of competence and motivation (pp. 598-608). New York: The Guilford Press.
Engeser, S. (Eds.). (2012). Advances in flow research. New York: Springer.
Engeser, S., & Rheinberg, F. (2008). Flow, performance and moderators of challenge -skill balance. Motivation and Emotion, 32(3), 158-172.
Fuchs, L. S., Schumacher, R. F., Long, J., Namkung, J., Hamlett, C. L., Cirino, P. T., Jordan, N.C., Siegler, R., Gersten, R., & Changas, P. (2013). Improving at-risk learners' understanding of fractions. Journal of Educational Psychology, 105(3), 683-700.
Kiili, K., Perttula, A., & Arnab, S. (2014). Flow in SGs. Public Deliverable 2.4, Games and Learning Alliance – The European Network of Excellence on Serious Games. <www.galanoe.eu>.
Kiili, K., Perttula, A., Lindstedt, A., Arnab, S., & Suominen, M. (2014). Flow Experience as a Quality Measure in Evaluating Physically Activating Collaborative Serious Games. International Journal of Serious Games, 1(3), 35-49.
Lieberman, D. A., Chamberlin, B., Medina, E., Franklin, B. A., Sanner, B. M., & Vafiadis, D. K. (2011). The power of play: innovations in getting active summit 2011 a science panel proceedings report from the American Heart Association.Circulation, 123(21), 2507-2516.
Link, T., Moeller, K., Huber, S., Fischer, U., & Nuerk, H. C. (2013). Walk the number line–An embodied training of numerical concepts. Trends in Neuroscience and Education, 2(2), 74-84.
McMullen, J., Laakkonen, E., Hannula-Sormunen, M., & Lehtinen, E. (2015). Modeling the developmental trajectories of rational number concept (s). Learning and Instruction, 37, 14-20.
Moeller, K., Fischer, U., Link, T., Wasner, M., Huber, S., Cress, U., & Nuerk, H. C. (2012). Learning and development of embodied numerosity. Cognitive processing, 13(1), 271-274.
Moyer, P. S., Bolyard, J. J., & Spikell, M. A. (2002). What are virtual manipulatives? Teaching children mathematics, 8(6), 372-377.
Ni, Y., & Zhou, Y. D. (2005). Teaching and learning fraction and rational numbers: The origins and implications of whole number bias. Educational Psychologist, 40(1), 27-52.
Pouw, W. T., Van Gog, T., & Paas, F. (2014). An embedded and embodied cognition review of instructional manipulatives. Educational Psychology Review, 26(1), 51-72.
Reimer, K., & Moyer, P. S. (2005). Third-graders learn about fractions using virtual manipulatives: A classroom study. Journal of Computers in Mathematics and Science Teaching, 24(1), 5-25.
Riconscente, M. M. (2013). Results from a controlled study of the iPad fractions gam Motion Math. Games and Culture, 8(4), 186-214.
Shute, V. J., & Kim, Y. J. (2014). Formative and stealth assessment. In J.M. Spector, M.D. Merrill, J. Elen, & M.J. Bishop (Eds.) Handbook of research on educational communications and technology (pp. 311-321). New York: Springer.
Shute, V. J. (2011). Stealth assessment in computer-based games to support learning. Computer Games and Instruction, 55(2), 503-524.
Siegler, R. S., Thompson, C. A., & Schneider, M. (2011). An integrated theory of whole number and fractions development. Cognitive psychology, 62(4), 273-296.
Siegler, R. S., Fazio, L. K., Bailey, D. H., & Zhou, X. (2013). Fractions: the new frontier for theories of numerical development. Trends in cognitive sciences, 17(1), 13 -19.
Stafylidou, S., & Vosniadou, S. (2004). The development of students’ understanding of the numerical value of fractions. Learning and Instruction, 14(5), 503-518.
Torbeyns, J., Schneider, M., Xin, Z., & Siegler, R. S. (2015). Bridging the gap: Fraction understanding is central to mathematics achievement in students from three different continents. Learning and Instruction, 37, 5-13.
Van Dooren, W., Lehtinen, E., & Verschaffel, L. (2015). Unraveling the gap between natural and rational numbers. Learning and Instruction, 37, 1-4.
Vamvakoussi, X., & Vosniadou, S. (2010). How many decimals are there between two fractions? Aspects of secondary school students’ understanding of rational numbers and their notation. Cognition and Instruction, 28(2), 181-209.
Wood, G., & Fischer, M. H. (2008). Numbers, space, and action–from finger counting to the mental number line and beyond. Cortex, 44(4), 353-358.