Mathematics Education Centre
Loughborough University
Email: l.j.alcock@lboro.ac.uk
Mathematics Education Centre
Loughborough University
Email: m.j.inglis@lboro.ac.uk
This article is about visual issues in the presentation of mathematics within teaching situations. It focuses particularly on the presentation of proofs to undergraduate students. We describe some of the decisions that a lecturer must make when presenting a written proof, from the layout of individual equations to the layout of a whole argument on the page. We consider the way in which these decisions are made explicit for lecturers who construct electronic learning resources termed e-Proofs, and conclude by discussing the constraints and affordances of this technology.
In some aspects of undergraduate teaching, visual considerations are naturally salient. Lecturers give presentations and, whether or not these use electronic presentation software, some thought is given to layout. Such considerations include how much to put on one page or board, what size the words should be, what to reveal at what stage, and simple practicalities such as how to use the space available so that all the students can see everything that is written. Lecturers might differ in the extent to which they attend to these considerations and the extent to which the result satisfies their students, but all make these choices on a day-to-day basis.
Visual considerations also have natural salience in some aspects of mathematics. In mathematics, one usually thinks of visual work as involving graphs or other types of diagrams, and a wealth of resources now exists to enhance our ability to create and animate visual images representing mathematical concepts and relationships. Some of these resources have been put to extensive use in teaching, and will be discussed briefly in the next section. This article, however, discusses a different issue, that of how lecturers present mathematical proofs.
A mathematical proof is, roughly speaking, a demonstration that a statement must be true, given established assumptions (axioms, definitions and laws of logic). Proofs are ubiquitous in higher-level mathematics, which has been characterised as “a proving science” (Hilbert, Renkl, Kessler, & Reiss, 2008). Given the central place that proofs occupy in mathematics, it is unsurprising that comprehending proofs is the most common learning activity in undergraduate mathematics classrooms (Weber, 2004). A stereotypical undergraduate mathematics lecture consists of the lecturer writing down successive definitions, theorems and proofs on a blackboard (or perhaps an overhead projector), coupled with verbal explanations and physical gestures designed to help the audience. Many in the mathematics community are highly attached to this mode of teaching (Baxter, 2005).
Here we concentrate on two distinct ways in which communication of mathematical proofs involves visual information: the layout of a mathematical proof on a page, and the gestures lecturers use to convey information about the structure of the proof. We consider the layout issue at three distinct levels: layout of systems of equations, layout of subarguments so as to highlight similar structures, and layout of proofs so as to facilitate the comprehension of the structure of the whole proof. We discuss layout choices that lecturers routinely make, and the compromises between choices at the different levels when deciding how to present any particular proof. We then highlight some ways in which gestures are naturally used to draw attention to the structures captured by any layout. Finally, we draw together discussion of these two kinds of visual information by considering how a particular type of resource, termed an e-Proof, encourages greater than usual attention to be paid to layout, and aims to capture information that would usually be conveyed by gesture in a lecture.
As noted in the introduction, discussions of the visual aspects of mathematics have primarily been associated with representations such as graphs and diagrams that are clearly of a visual nature. One line of research in this area has focused on whether some individuals have a preference for visual reasoning, and the consequences if they do (Alcock & Simpson, 2004; Dreyfus, 1994; Presmeg, 1986). Another, particularly in the context of calculus, has focused on whether students can accurately “read off” information from graphical representations, and what sort of representation might facilitate conceptual understanding of concepts such as the derivative (Tall, 1992). Another has focused on ways in which students and teachers interact with dynamic geometry software (Jones, 2000). Such software facilitates the construction and direct manipulation of geometric figures, but one problem is that the immediacy and sense of obviousness obtained by manipulating figures on screen do not translate easily into the motivation to establish the logical relationships embodied by the figures (Hadas, Hershkovitz, & Schwarz, 2000). Thus in this strand of research, as in others (Zazkis, Dubinsky, & Dautermann, 1996), some authors have argued that ability to translate between visual and other representations is required for successful visual thinking in mathematics.
This is not the only approach to such issues, however. Giaquinto (2007), for instance, argued that the distinction between “visual thinking” and some contrasting type (often called “algebraic”, “symbolic” or “analytic” thinking) may be false, not because the focus should be on the translation between representation systems, but because for some representation systems it is not easy to make this classification. He suggested that there may be “several independent features whose presence or absence unconsciously affects our inclination to classify thinking as symbolic or diagrammatic” (p.259), and cited commutative arrow diagrams as a case which is visual in the sense that “relationships are simultaneously displayed rather that sequentially stated” (p.256) but for which there is also a syntax. Importantly for our discussion, he also argued that algebraic manipulation involves visual experience in two significant ways: first, because algebraic manipulation involves imagery of sliding, rotating and so on (when manipulating algebraic expressions, we might consider ourselves to be moving all the x’s to the left or swapping the physical positions of two symbols), and, second, because deciding what to manipulate (and how) involves recognising structures in written mathematics at various levels. For instance, he considered an expression 
to have primary form 
and non-primary form 
. In the non-primary form, “
” is treated as a single unit which can be acted upon; seeing it this way requires shifting one’s attention and so as not to be distracted by its component parts. Giaquinto noted that making progress in algebraic derivations with such expressions involves making shifts of visual aspect between such forms (p. 199).
Researchers have investigated the degree to which students notice what Giaquinto called non-primary forms. In mathematics education, the ability to do this is sometimes called “structure sense” and is related to the ability to see an expression as a single object rather than as a process to be carried out (Gray & Tall, 1994; Linchevski & Livneh, 1999; Sfard & Linchevski, 1994). Structure sense has been studied via cases in which a problem or exercise is straightforward if one sees the structure, but requires a lengthy chain of manipulations if attention is focused on the primary form. For instance, Hoch and Dreyfus (2005) studied 15-year-old students’ ability to answer items such as factoring the expression 
. Only 23 out of 88 participants treated 
as a single variable and made use of the non-primary quadratic structure; many more (57) opened the brackets as a first move, attending instead to the primary structure.i
In mathematics education and psychology, researchers have also focused on the impact of visual information on students’ tendency to make or endorse incorrect algebraic “moves”. Kirshner and Awtry (2004), for instance, studied cases in which the salience of certain visual information is related to common errors in algebra. They observed that the many typical “mal-rules” applied by students, such as 
, are analogous in form to correct rules (in this case 
), and that such rules have visual coherence in the sense that the left- and right-hand sides appear naturally related to one another. They suggested two characteristics that contribute to this coherence of such (so-called ‘visually salient’) mal-rules: “repetition of elements across the equals sign and a visual reparsing of elements across the equal sign” (p. 229). In contrast, some genuine rules lack visual salience and are therefore particularly difficult for students to accept, for example, 
.
In a separate line of research, Landy and Goldstone (2007) found that, contrary to various processing models of algebraic performance, the physical spacing of algebraic and arithmetic expressions influences how students engage with them. For example, when spacing respects the order of operations (e.g., 
) it is easier to process than when the spacing is reversed (e.g., 
).
Clearly, making use of visual information is important in interpreting notation correctly and in performing productive algebraic manipulations. Our discussion in this article moves further in the direction of considering the visual impact of the way in which symbols and words are laid out on a page, this time in situations in which the immediate aim is for the student to understand an extended argument rather than to manipulate symbols. Thus, we shall argue that while a proof like that shown in Figure 1 would not ordinarily be thought of as involving “visual” mathematics, in fact there are many visual issues worth consideration in its presentation.
Figure 1. A theorem and proof from an undergraduate mathematics course (screen taken from an e-Proof).
In undergraduate mathematics lectures, lecturers state and prove theorems. Both the theorems and the proofs are typically written using a combination of words and algebraic notation, the proportions of each varying with the subject matter and with the individual preference of the lecturer. The amount of both verbal and symbolic abbreviation also varies, but in most cases both the theorem and proof will be written so that, provided that the reader is familiar with the notation, they could read the whole out loud as they would read out any other coherent text. In this section we consider ways in which the visual layout of a proof might impact its readability to a novice audience and must be decided by a lecturer.
Proofs often involve sequences of algebraic manipulations. The layout of these manipulations is under the control of the lecturer but is subject to competing constraints. For instance, the argument below is composed of a series of inequalities linked by logical equivalence symbols (
):
This structure may be more discernible with extra spaces and longer arrows:
This may be related to the effect Giaquinto discussed (Giaquinto, 2007, p.200) in which information is seen to be in columns or not depending upon the layout. Here it may be that the inequalities can be more readily seen as chunks with the additional separation.
Layouts that are more recognisably in columns are also used. For longer chains of equations or inequalities, for instance, a horizontal layout can be visually confusing, as figure 2 illustrates.
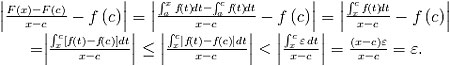
Figure 2. A visually confusing layout for a chain of inequalities.
A vertical layout is commonly used in such situations. This tends to mean that symbols that are being replaced by others are more closely lined up underneath each other. It also allows more space for adding reasons for given relationships, as illustrated in Figure 3.
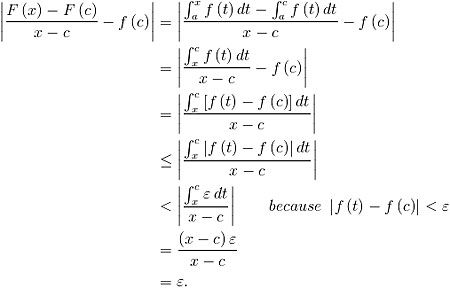
Figure 3. A vertical layout for a chain of inequalities.
Mathematical typesetting packages allow routine use of such vertical layouts, and it might seem obvious that they should always be used in similar cases. However, in undergraduate mathematics such a chain of equalities would often be embedded within a longer proof. This longer argument might have higher-level structure which is more difficult to see if key elements are more separated on the page, as we discuss in the next sections.
Proofs can often be thought of as composed of sections of which each establishes some step in the whole argument. Sometimes two or more of these have a similar structure, and recognition of this might reduce the apparent complexity of the argument for a reader. For example, consider the proof from Figure 1. This has two places in which very similar reasoning is used twice, both of which are highlighted in Figure 4. In the first, it is established that 
then that 
. This takes one line each time and the matching layout on these two lines is designed to facilitate the recognition of this. In the second, it is established that 
and then that 
. This takes two lines each time and, in the second case, involves an additional comment in the argument. Again, however, the largely matching layout is designed to facilitate recognition of this difference.
Figure 4. Proof with blocks of repeated reasoning highlighted.
As with the discussion of equation layout in the previous section, it might seem obvious that where structures “match”, this matching should be reflected in the layout on the page. This often happens by default, since in many cases lecturers start a new line every time they start a new sentence. Some textbooks also use this general tactic when presenting proofs (see, for example, the proofs in the appendix of J. Stewart’s (2008) Calculus). This peculiarity of mathematical writing separates each deduction but also means that similar elements do tend to appear lined up. This does not always happen, however: many undergraduate textbooks present proofs in continuous paragraph text (e.g., Stewart & Tall, 1977).
However, modifying a layout to highlight similarities may not have straightforward benefits. On the one hand, it might reduce the amount of work that a student has to do to “see” similar steps in the argument. On the other, it is well known that students often learn mathematics by attending to syntactic regularities without understanding the underlying meaning (e.g., Lithner, 2003). The salience of the matching might exacerbate this tendency and thus impede understanding of the proof as a whole, as discussed in the following sections.
In order to understand a mathematical proof fully, it is not sufficient to understand each statement in isolation. One also needs to understand how the statements fit together to form a coherent and logically valid argument. The thinking this might involve can be illustrated by considering Figure 4 again. The second highlighted box is preceded by a line saying
Now we shall prove that 
.
and followed by a line that begins
Hence …
The point of the section in the box is that it achieves this stated aim of showing that , and in order to understand the proof fully one would need to recognise this. The proof achieves this aim by showing that 
cannot be less than or greater than 
. It does this via the two subproofs, each of which leads to a contradiction of the earlier statement that 
is the supremum of the set X. In order to understand fully, one would need to work out what exactly has been contradicted. This requires the reader to input previous knowledge of the definition of supremum and to refer to the point earlier in the proof at which X is defined in order to work out how it applies to give the contradiction in this case.
Various devices are used in mathematical writing to draw attention to this kind of structure. Statements of intent (“Now we shall prove that 
.”) are one such device. Another is to label part of the proof and to refer back to it later. For instance, one might put an asterisk by the third line where the set X is defined and refer to this to give a more detailed explanation of how exactly the contradiction arises. However, such additional information would increase the length of the proof, and it is rarely the case that every such structural element is specifically flagged and explained. So the reader necessarily has to do some work to identify this type of higher-level structure. Learning to do so is perhaps analogous to learning structure sense as discussed earlier.
There are practical trade-offs among the constraints discussed in the above sections. Using a vertical rather than horizontal layout for a system of equations increases the apparent length of a proof. This might interfere with the identification of structures at higher levels because parts of an argument that are logically connected will be physically more separated in space, especially if the length is pushed above one page.
Mathematicians routinely make decisions about such trade-offs as part of their teaching practice. Indeed, they probably do so more consciously now that technology facilitates the production and distribution of printed and on-screen notes. The impact of layout in these notes is greater now for the same reason, since students have access to the materials exactly as the lecturer intended and not in their own handwritten copy in which layout might vary. Nevertheless, lecturers likely make these layout decisions in an ad hoc, responsive way, deciding “what looks good” for any given proof, without systematically considering the alternatives.
There is no need to alter this model if we assume that the student should be able to identify the structures from any layout. Mathematicians might reasonably see such work as a necessary part of coming to understand a proof, although students may not aim for the level of understanding that a mathematician would consider appropriate (Selden & Selden, 2003; Weber, 2008). However, proof comprehension is a complex task involving coordinating information at different levels, if not simultaneously then at least in quick succession (Weber & Alcock, 2005; Yang & Lin, 2008). As a result, a student’s success in understanding any given proof is likely to be affected by problems of cognitive load. Whether high loads can be reduced by simple manipulations of layout is an open question, and we shall return to this point later.
A lecturer typically says much more than they write (or show) by giving rationales for construction of the proof in a certain way, reminders of the meanings of basic concepts, links to other parts of the course, etc. Much of this speech will likely be accompanied by gestures, which therefore constitute another form of visual information available to students.
Like all communicators, lecturers make a variety of different types of gesture. For example, Greiffenhagen (2008) analysed a lecture from a course on inductive logic, and found that the lecturer made gestures (among others):
to make a small upwards movement while pointing at one of the quantities and discussing another that is “slightly bigger” (Greiffenhagen, 2008).
Such gestures reflect the content of the mathematics in a meaningful way. Research involving much younger students indicates that they can pick up mathematical ideas conveyed through gesture. Such research has used procedures for solving very simple problems (of the type 
), and has shown that children in individual instruction are more likely to reiterate the teacher’s speech if it is accompanied by a matching gesture than no gesture, and less likely still if the gesture conflicts with the conceptual structure (Goldin-Meadow, Kim, & Singer, 1999). Furthermore, children required to produce gestures consistent with an appropriate strategy tended to learn more than those required to produce partially correct gestures, and these, in turn, tended to learn more than those required to produce no gestures (Goldin-Meadow, Cook, & Mitchell, 2009).
The message of this research is that gestures are not incidental in mathematical learning: teachers’ gestures aid their students’ learning, and students’ gestures during learning activities aid retention. Critically, however, during undergraduate lectures, lecturers’ gestures are usually not recorded (either in student’s self-taken notes, or in written handouts produced by lecturers), and students in lectures are not often (if ever) taught to gesture in a systematic way.
In the next section we discuss e-Proofs, a novel computer-based approach to presenting mathematical proofs that does attempt to record information usually encoded in gestures, as well as make explicit other types of information about mathematical structures as discussed in the earlier sections.
E-Proofs are designed with the intention of supporting students both in comprehension of particular proofs and in developing an awareness of the logical structures they should attend to when reading proofs in general. In the current iteration, each e-Proof has an underlying copy of a theorem and proof, multiple screens in which various sections are “greyed out” to focus attention on particular parts and, for each screen, a verbal commentary with boxes and arrows that appear and disappear to highlight the relationships described therein.
Figures 5, 6 and 7 illustrate the way in which an e-Proof synchronises audio commentary and visual information. The figures show three images from one screen, demonstrating how the annotations change as the audio progresses; the commentary is reproduced in the captions.
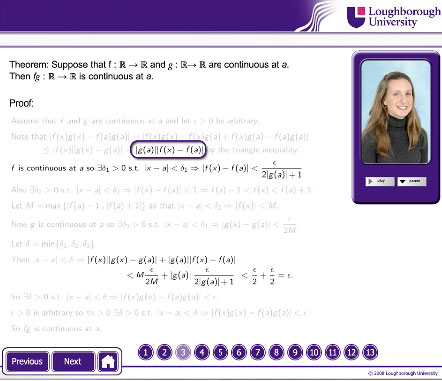
Figure 5. “In the third line, we work on the second part of our expression above. We start here because this part is simpler to deal with”.
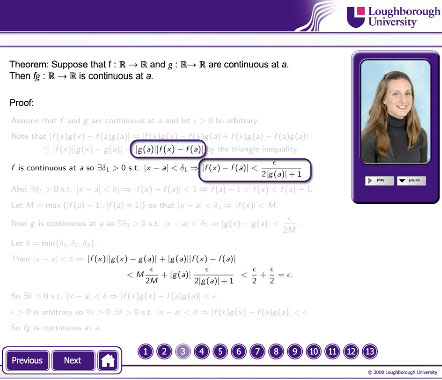
Figure 6. “At the end of the line, we see that we have mod of f of x minus f of a is less than epsilon over two mod g of a plus 1”.
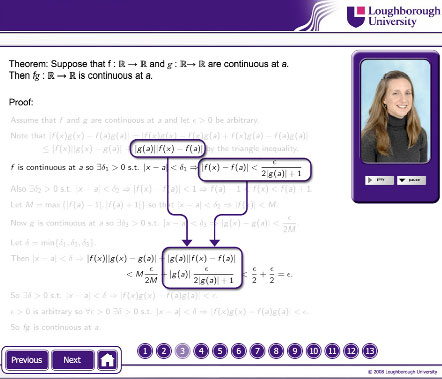
Figure 7. “This is because we want to end up with mod g of a times mod f of x minus f of a less than epsilon over 2, and we want to avoid a situation where we are dividing by zero”.
These figures illustrate the way in which the animations and audio can be used to focus attention on the way statements within a proof are coordinated in a higher-level structure. Some of the other explanations focus instead on providing detailed explanations of a single line. Along with other e-Proofs, the version shown in Figures 5–7 is currently on the university’s VLE page for the relevant course. Students can interact with it in a number of ways: they can move from screen to screen using either the back and next buttons on the bottom left or the number buttons along the bottom; they can play the audio by clicking the play button under the lecturer’s picture on the right; and they can pause this when they want to and play it multiple times (or not at all). This e-Proof was made using Flash and the full working version can be seen and tried out at http://www.projectexpound.org.uk/ i
The creation of e-Proofs encourages consideration of visual issues in a way that the planning of ordinary lecture presentations does not. This operates on all the levels discussed in the sections on layout and gesture, and we shall now run through these (in the reverse order).
First and perhaps most obviously, information that would normally be conveyed in gesture is converted to a combination of annotations and highlighting. Constructing the annotations and highlights in advance encourages the lecturer to decide explicitly where they want to focus attention. The first author has argued (Alcock, 2009) that e-Proofs provide a more precise way of directing attention than would normally be achieved by spontaneous gestures, and that they capture this information so that it remains available once the lecture is over.
This way of capturing gestures means that information that is normally implicit in a written proof can be made explicit. Logical structures that cut across the proof can be highlighted, either as part of a line-by-line explanation or in separate screens designed to focus attention at this higher level. Similar subarguments can be explicitly pointed out, either by focusing on their internal similarity or by focusing on the way in which they contribute to a higher-level argument (Figure 8 shows an example of the latter, from the older style e-Proof used earlier in Figures 1 and 4). Again, a lecturer constructing an e-Proof needs to make decisions in advance about where to focus attention and how.
Figure 8. An e-Proof screen focusing attention on the structure of the subargument showing that , as discussed earlier.
This use of annotations and highlighting means that in some ways, e-Proofs make visual information more salient than does an ordinary lecture or written presentation. They are designed to use such information to focus students’ attention, and a lecturer designing an e-Proof is encouraged to make more advance, conscious decisions about what visual information to include. However, the physical constraints imposed by font and page size are much less forgiving than in printed lecture notes or in a presentation at the board. While this could be offset by features that allow zooming or moving around within the text, we decided at this stage to prioritise maintaining a sense that the proof is a whole argument by keeping it all displayed at once. This restriction means that there are fewer options in deciding on the layout of equation systems or parts of the proofs so that similar structures are lined up. For proofs of the length shown here, it also means that there is a finite amount of space for statements of intent and other indicators of structure that might have appeared in ordinary printed or written lecture notes. These indicators can instead be captured by annotations and audio, but there is a trade-off in what can be included in what form, especially when one considers that the navigation facilities also take up space.
E-Proofs provide more information than a written copy of the underlying proof. However, they do not provide a great deal more: typically only one short explanation is offered for each statement or logical relationship. In a lecture, something quite different happens: multiple explanations are offered at speed, with ongoing gestures and with information at different levels mixed together. Study of an e-Proof might therefore improve a student’s learning by allowing them to process a manageable amount of information at a time, or it might detract from it by denying them access to multiple versions of the same explanation. In a written presentation, something different happens again: no extra explanation is provided, so readers must decide where to focus and construct explanations on their own. Study of an e-Proof might therefore improve students’ learning by giving them explanations that they would not otherwise construct, or it might detract from them by removing the need to think deeply about what a suitable explanation would involve.
It is not clear how such concerns should be balanced in pedagogical practice, and therefore not clear whether and to whom e-Proofs in their current form will be beneficial. Some opinions are consistent with the idea that support for taking in explanations is needed: students often claim that it is impossible to write everything down in an ordinary mathematics lecture while also trying to understand what is said. Other opinions are consistent with the idea that offering too much support undermines learning: lecturers often believe that if students do not have something to do they will drift off, and research indicates that taking notes does increase retention of presented information, (Kiewra, 1989) (though it is not obvious how this applies in the common situation in mathematics lectures in which students write down exactly what the lecturer writes and no more). It is also possible that e-Proofs or similar resources may be of great use to new undergraduates who are unaccustomed to reading proofs, but of minimal use or even detrimental at higher levels.
Further investigation is therefore needed to ascertain whether e-Proofs benefit students at different levels in different ways and, indeed, whether different formats (with more or less explanation, or prompts for students to consider explanations of their own) would be more useful. To facilitate this and to allow lecturers to produce e-Proofs of their own, work is now underway to construct a web-based e-Proof creation tool called ExPOUND. This tool will allow choices about e-Proof layout and will also allow text and diagrams to appear and disappear either over the proof or off to one side. For more detail see http://expound.lboro.ac.uk.
Visual information is abundant in mathematics, even in presentations of verbal/symbolic arguments that are not typically thought of as involving visual representations. Here we have suggested that written proofs visually encode structures and relationships at various levels, and that decoding this information to retrieve these structures is an important part of understanding undergraduate mathematics. Similarly, gestures embody information about mathematical objects, relationships between them, and (the aspect that is captured in e-Proofs) indicators as to which part of a proof is supposed to be the focus of attention and how it is related to other parts.
Some of this visual information is thought about consciously by mathematics lecturers, and other parts not. Lecturers make many decisions about layout in any written presentation, but they may not have any systematic rationales for these decisions, even though the outcomes are likely to be increasingly influential now that at least some pre-printed notes are commonly provided. Similarly, while a lecturer might sometimes decide to point deliberately or to use a gesture intended to represent an object or relationship, many gestures used will be simply integrated as part of ordinary communication.
Constructing e-Proofs encourages a lecturer to think deliberately about the visual information provided on top of a written format, and allows students to access this extra information at their own pace. Extra resources with such facilities are often popular, and informal feedback from a second- and third-year course in Analysis indicated that students liked e-Proofs, felt that they understood proofs better when these were available, and would have liked more to be available across different courses (Alcock, 2009). Similarly, feedback from mathematics lecturing staff who have seen the e-Proof system has been positive. Nevertheless, informal feedback has serious limitations and does not, in particular, demonstrate effectiveness. Further research is planned to compare the learning gains achieved by students studying with e-Proofs with the gains made by those restricted to using traditional paper-based notes.
This work was partially supported by grants from JISC and the MSOR Network.
Alcock, L. (2009). e-Proofs: Student experience of online resources to aid understanding of mathematical proofs. In Proceedings of the 12th Conference on Research in Undergraduate Mathematics Education. Raleigh, NC: Special Interest Group of the Mathematical Association of America on Research in Undergraduate Mathematics Education.
Alcock, L., & Simpson, A. (2004). Convergence of sequences and series: Interactions between visual reasoning and the learner’s beliefs about their own role. Educational Studies in Mathematics, 57(1), 1-32.
Baxter, P. D. (2005). One year on — reflections of new lecturer. MSOR Connections, 5(2) , 1-3.
Dreyfus, T. (1994). Imagery and reasoning in mathematics and mathematics education. In D. F. Robitalle, D. H. Wheeler, & C. Kieran (Eds.), Selected Lectures from the 7th International Congress on Mathematical Education (pp. 107-122). Quebec, Canada: Les Presses de l’Université Laval.
Giaquinto, M. (2007). Visual thinking in mathematics. Oxford: Oxford University Press.
Goldin-Meadow, S., Cook, S. W., & Mitchell, Z. A. (2009). Gesturing gives children new ideas about math. Psychological Science, 20(3), 267-272.
Goldin-Meadow, S., Kim, S., & Singer, M. (1999). What the teacher’s hands tell the student’s mind about math. Journal of Educational Psychology, 91(4), 720-730.
Gray, E., & Tall, D. (1994). Duality, ambiguity and flexibility: A proceptual view of simple arithmetic. Journal for Research in Mathematics Education, 25(2), 115-141.
Greiffenhagen, C. (2008). Video analysis of mathematical practice? Different attempts to “open up” mathematics for sociological investigation. Forum: Qualitative Social Research, 9(3), 32.
Hadas, N., Hershkovitz, R., & Schwarz, B. B. (2000). The role of contradiction and uncertainty in promoting the need to prove in dynamic geometry environments. Educational Studies in Mathematics, 44(1-2), 127-150.
Hilbert, T. S., Renkl, A., Kessler, S., & Reiss, K. (2008). Learning to prove in geometry: Learning from heuristic examples and how it can be supported. Learning and Instruction, 18(1), 54-65.
Hoch, M., & Dreyfus, T. (2005). Students’ difficulties with applying a familiar formula in an unfamiliar context. In H. L. Chick & J. L. Vincent (Eds.), Proceedings of the 29th International Conference on the Psychology of Mathematics Education (Vol. 3, pp. 145-152). Melbourne, Australia: IGPME.
Jones, K. (2000). Providing a foundation for deductive reasoning: Students’ interpretations when using dynamic geometry software and their evolving mathematical explanations. Educational Studies in Mathematics, 44(1-2), 55-85.
Kiewra, K. A. (1989). A review of note-taking: The encoding storage paradigm and beyond. Educational Psychology Review, 1(2), 147-172.
Kirshner, D., & Awtry, T. (2004). Visual salience of algebraic transformations. Journal for Research in Mathematics Education, 35(4), 224-257.
Landy, D., & Goldstone, R. (2007). How abstract is symbolic thought? Journal of Experimental Psychology: Learning, Memory and Cognition, 33(4), 720-733.
Linchevski, L., & Livneh, D. (1999). Structure sense: The relationship between algebraic and numerical contexts. Educational Studies in Mathematics, 40(2), 173-196.
Lithner, J. (2003). Students’ mathematical reasoning in university textbook exercises. Educational studies in mathematics, 52(1), 29–55.
Presmeg, N. C. (1986). Visualisation and mathematical giftedness. Educational Studies in Mathematics, 17(3), 297-311.
Selden, A., & Selden, J. (2003). Validations of proofs considered as texts: can undergraduates tell whether an argument proves a theorem? Journal for Research in Mathematics Education, 34(1), 4-36.
Sfard, A., & Linchevski, L. (1994). The gains and the pitfalls of reification — the case of algebra. Educational Studies in Mathematics, 26(2), 191-228.
Stewart, I. N., & Tall, D. O. (1977). The foundations of mathematics. Oxford: Oxford University Press.
Stewart, J. (2008). Calculus. Toronto, Brooks/Cole.
Tall, D. O. (1992). Visualizing differentials in two and three dimensions. Teaching Mathematics and its Applications, 11(1), 1-7.
Weber, K. (2004). Traditional instruction in advanced mathematics courses: A case study of one professor’s lectures and proofs in an introductory real analysis course. Journal of Mathematical Behavior, 23(2), 115-133.
Weber, K. (2008). How mathematicians determine if an argument is a valid proof. Journal for Research in Mathematics Education, 39(4), 431-459.
Weber, K., & Alcock, L. (2005). Using warranted implications to understand and validate proofs. For the Learning of Mathematics, 25 (1), 34-38.
Yang, K.-L., & Lin, F.-L. (2008). A model of reading comprehension of geometry proof. Educational Studies in Mathematics, 67(1), 59-76.
Zazkis, R., Dubinsky, E., & Dautermann, J. (1996). Co-ordinating visual and analytic strategies: A study of students’ understanding of the group D4. Journal for Research in Mathematics Education, 27(4), 435-457.
i This e-Proof was created by Lee Barnett and with the support of a Loughborough University Academic Practice Award. The ExPOUND website gives information about a follow-on project supported by a JISC Learning and Teaching Innovation Grant.
Proofs can often be thought of as composed of sections of which each establishes some step in the whole argument. Sometimes two or more of these have a similar structure, and recognition of this might reduce the apparent complexity of the argument for a reader. For example, consider the proof from Figure 1. This has two places in which very similar reasoning is used twice, both of which are highlighted in Figure 4. In the first, it is established that then that . This takes one line each time and the matching layout on these two lines is designed to facilitate the recognition of this. In the second, it is established that and then that. This takes two lines each time and, in the second case, involves an additional comment in the argument. Again, however, the largely matching layout is designed to facilitate recognition of this difference.